(The original article was run in the Chicago Tribune, registration required.)
Take a minute to walk through this technique:
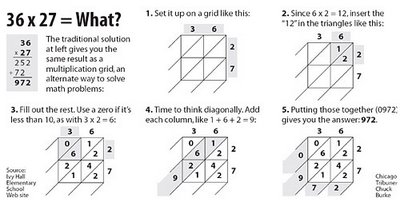
**Note: the following material is my original work, not a re-posting.**
The grid approach is not without that pesky requirement to "carry" ones. It is merely a re-arrangement of traditional multiplication. (Trust me, it is: the "proof" is too nerdy to endure!)
The C-trib illustrators inadvertently cause a pitfall for students of the new technique when they start diagonal addition from the left. One small adjustment solves the discrepancy: begin addition from the right.
Ask yourself: can you think of a combination of two 2-digit numbers for which at least one of the diagonal sums is greater than 10? If you can, you've just demonstrated to yourself the need to begin diagonal addition from the right, carrying 'extra' ones leftward, as is with the traditional approach. See my illustration below:

The first result occurs when diagonal addition begins at the left; illustrated at right is the intended result, having carried the ones: 78 x 59 = 4602.
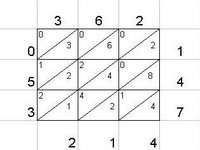
Continuing the algorithm just a little farther into application, we see that it still works when applied to three-digit products (example, 362 x 147 = 53214):
And, with nerdy satisfaction, I proudly report to all two of my readers that I did this just for fun!
My favorite Calculus professor (pictured) taught us about a Latin abbreviation commonly used to signify the close of a proof: Q.E.D. (Quod Erat Demonstratum). I much prefer the mnemonic device he taught us to remember it, tongue in cheek: "Quite Easily Done."
technorati tags: Chicago Tribune, teaching math, multiplication, learning, Dr. Eric Lund, 37signals, Quod Erat Demonstratum, Tommi Godwin
4 comments:
One of the numerous reasons I love you so much. I love the way you think.
My so unexpert opinion about this is that new math methods have been tried and they have failed to come into being. The people who teach, must know and understand what it is they are teaching. If they aren't confident in that, they will not support the method. New math methods follow a rule that is, if it ain't broke, don't learn something else.
I like this, it gets you thinking, but really, I don't see it going much further.
It is so YOU to "play" with numbers and thinking in a manner much like a cat might play with a mouse. In the end, the cat wins! I like that about you. What you might like about me is that I followed you all the way through this discussion - only fair in light of the many conversations about education through which you've followed me.
I love you, Peanut.
-mg
Oh, and btw... I picked up that link to automatic bibliographic entries... love it!! -mg
Post a Comment